Helmholtz-Spule: Kompletter Leitfaden zur Erzeugung eines gleichmäßigen Magnetfelds

Wichtige Erkenntnisse

• Eine Helmholtz-Spule besteht aus zwei identischen kreisförmigen Spulen, deren Abstand dem Spulenradius entspricht. In der Mitte entsteht ein nahezu gleichförmiges Magnetfeld.

• Benannt nach Hermann von Helmholtz, ist diese Anordnung in Forschung und Messtechnik weit verbreitet, wenn präzise Magnetfeldkontrolle erforderlich ist.

• Varianten ermöglichen gleichförmige Felder (Helmholtz) oder kontrollierte Gradienten (Anti-Helmholtz).

• Anwendungen: Kompensation des Erdmagnetfelds, Kalibrierung sensibler Sensoren, Messung magnetischer Momente, biomedizinische und materialwissenschaftliche Untersuchungen.

• Die Feldstärke im Zentrum folgt aus dem Biot-Savart-Gesetz und hängt von Radius R, Windungszahl N, Strom I und μ0 ab.

Einordnung und Nutzen

Wenn Experimente eine definierte, reproduzierbare magnetische Umgebung erfordern, bietet das Helmholtz-Spulenpaar eine elegante, gut berechenbare Lösung. Durch die gezielte Geometrie entsteht im zentralen Volumen ein Feld hoher Gleichförmigkeit – ideal für Kalibrierungen, Vergleichsmessungen und Grundlagenversuche.

Was ist eine Helmholtz-Spule?

Eine Helmholtz-Spule besteht aus zwei identischen, koaxialen Spulen mit gleicher Stromrichtung. Der Spulenabstand entspricht dem Radius R. Dadurch überlagern sich die Einzelfelder so, dass Feldgradienten niedriger Ordnung im Zentrum minimiert werden und ein homogenes Feld in einem nutzbaren Volumen entsteht.

Vorteil gegenüber Einzelspulen: Höhere Feldgleichförmigkeit über ein größeres Volumen bei moderater Baugröße und einfacher Berechenbarkeit.

Magnetfeldtheorie und Berechnung

Die Berechnung basiert auf Biot-Savart und Superposition. Für das Feld im Zentrum eines idealen Helmholtz-Spulenpaars gilt:

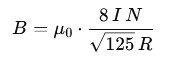
Wobei:

• B die magnetische Flussdichte darstellt
• μ₀ die magnetische Permeabilität des freien Raums ist (4π × 10⁻⁷ T⋅m/A)
• N die Anzahl der Windungen pro Spule ist
• I der Spulenstrom ist
• R der Radius der Spulen ist

Implikation: B​ ist proportional zu N und I und inverse proportional zu R.

Feldverlauf entlang der Achse

Die maximale Feldstärke liegt im geometrischen Mittelpunkt zwischen den Spulen. Entlang der Zentralachse nimmt das Feld vom Zentrum aus sanft ab. Der gleichförmige Bereich umfasst approximativ ein kugelförmiges Volumen von rund ≈ 20 % des Spulenradius im Durchmesser, innerhalb dessen die Feldabweichung typischerweise < 1 % bleibt (design- und toleranzabhängig).

Hinweis zur Theorie: Im Zentrum verschwinden die Ableitungen niedriger Ordnung (Taylorentwicklung), was die hohe Gleichförmigkeit erklärt.

Reale Spulen (endliche Dicke)

Praktische Spulen besitzen endliche Wicklungspakete (rechteckiger Querschnitt). Wichtig ist, den Abstand der Mittellinien zu definieren (nicht der Außenkanten). Wicklungslagen, Isolationsdicken und Leiterpositionen beeinflussen das real erzielte Feld leicht; präzise Mechanik verbessert die Übereinstimmung mit der Theorie.

Varianten und Konfigurationen

Quadratische Helmholtz-Spulen

Quadratische Leiterwege bieten größeres Innenvolumen und gute Zugänglichkeit. Die erreichbare Gleichförmigkeit ist vergleichbar, die Feldstärke bei gleichem Umfang etwas geringer. Der optimale Abstand ist geometrieabhängig; Designleitfäden verwenden hierfür empirisch/theoretisch bestimmte Faktoren. Einsatz z. B. bei Feldkompensation oder großen Prüfkörpern.

Maxwell-Konfiguration (Drei-Spulen-System)

Eine dritte, koaxiale Spule mit passenden Abständen/Windungsverhältnissen kann die Gleichförmigkeit über ein größeres Volumen weiter erhöhen (Kompensation höherer Ableitungen). Konkrete Parameter sind designspezifisch und werden nach Ziel-Toleranzen und Baugrößen festgelegt.

Anti-Helmholtz (Gradientenfeld)

Bei entgegengesetzter Stromrichtung in einer der Spulen entsteht im Zentrum ein Nullfeld und ein nahezu linearer Gradient im Nahbereich. Der Spulenabstand wird in der Praxis nahe dem Radius gewählt und für die gewünschte Gradientenlinearität optimiert (Anwendungs- und Geometrieabhängigkeit).

Strom- und Spannungsanforderungen

Gleichstrombetrieb (DC)

DC-Labornetzteile liefern stabilen Strom; die notwendige Spannung ergibt sich aus dem Widerstand der Wicklung (Drahtquerschnitt, Länge, Geometrie). Stromstabilität ist entscheidend, da ΔI direkt ΔB verursacht.

Hochfrequenzbetrieb (AC/HF)

Mit steigender Frequenz dominiert die induktive Reaktanz (XL=2πfL); zur Aufrechterhaltung des Stroms ist eine höhere Spannung nötig. Serienresonanz (mit Kondensator) kann die Reaktanz kompensieren. Grenzen setzen Leitungseffekte, Wirbelströme in Nachbarleitern und Inhomogenitäten durch mechanische Details. Praktische Obergrenzen liegen je nach Bauform im kHz–MHz-Bereich.

Anwendungen

Feldkompensation und Nullfeld-Umgebungen

Durch Überlagern eines Gegenfelds lässt sich das Erdmagnetfeld (≈ 25–65 µT) lokal stark reduzieren. Für vollständige Kompensation in allen Richtungen nutzt man drei orthogonale Helmholtz-Paare, ggf. mit aktiver Regelung (Sensorsignal → Stromnachführung).

Dreidimensionale Feldkontrolle

Drei orthogonale Paare ermöglichen beliebige Feldvektoren und rotierende Felder. Aktive Kompensation stabilisiert die Bedingungen in störbehafteten Umgebungen.

Messung magnetischer Dipolmomente

Helmholtz-Spulen liefern die gleichförmige Feldumgebung für Flux-Messungen (z. B. Magnet-Ausziehmethode). Über die Spulenkonstante (aus Kalibrierung) lassen sich Momente präzise bestimmen.

Konstruktionsleitlinien und Optimierung

• Spulenabstand: Theoretisch d≈Rd für Helmholtz. Kleinste Fertigungsfehler im Abstand erzeugen ≈ 0,5× Fehler in B → präzise Mechanik ist wichtig. Leicht größerer Abstand ist oft toleranzfreundlicher (etwas weniger B, etwas mehr Gleichförmigkeit).

• Drahtquerschnitt & Thermik: Größerer Querschnitt → weniger Widerstand, höherer Strom, mehr B; aber Geometrieänderung beachten (Abstand der Mittellinien bleibt Referenz). Wärmeabfuhr (Leiter, Träger) dimensionieren.

• Stützstrukturen: Nichtmagnetische Materialien (z. B. Kunststoffe, Holz, Aluminium ohne ferromagnetische Anteile) vermeiden Feldverzerrungen.

• Gleichförmigkeitszone: Prüfkörper vollständig im homogenen Volumen positionieren; bei größeren Objekten ggf. Maxwell-Erweiterung oder quadratische Geometrie erwägen.

Kalibrierung und Verifikation

Analytik ist ein guter Startpunkt, die experimentelle Kalibrierung bleibt jedoch unverzichtbar.

• Messmittel: Hall-Sensoren und Präzisions-Magnetometer erfassen B im Zentrum und in Off-Center-Punkten.

• Spulenkonstante: Verbindung zwischen Strom und Feld wird empirisch bestimmt; Lineariät über den Betriebsbereich prüfen.

• Referenzen: Rückführbare Standards (z. B. Nickel-Proben) sichern Genauigkeit.

• Wartung: Regelmäßige Kalibrierintervalle festlegen, Umgebungsbedingungen dokumentieren.

Häufig gestellte Fragen (FAQ)

Warum ist der Spulenabstand gleich dem Radius?
So werden niedrigere Feldableitungen im Zentrum minimiert; das führt zu einer hohen Gleichförmigkeit im nutzbaren Volumen.

Können Helmholtz-Spulen das Erdmagnetfeld vollständig kompensieren?
Mit einem Paar nur entlang einer Achse. Für vollständige Kompensation benötigt man drei orthogonale Paare und idealerweise aktive Regelung.

Was passiert bei ungleichen Strömen?
Asymmetrie verringert die Gleichförmigkeit deutlich. Reihenschaltung beider Spulen ist bevorzugt, um identische Ströme sicherzustellen.

Wie beeinflusst die Drahtstärke das Feld?
Größerer Querschnitt ermöglicht höhere Ströme (mehr B) bei geringerer Erwärmung, verändert aber die effektive Geometrie. Abstände stets über Mittellinien definieren.

Was begrenzt die maximale Betriebsfrequenz?
Induktive Reaktanz, Leitungseffekte und Wirbelströme. Praktische Grenzen liegen je nach Aufbau im kHz–MHz-Bereich.